使用Solver軟體進行德州撲克GTO研究時，最常見的問題之一是「為什麼Solver軟體會採取這個行動，明明別的行動的EV更高？」例如，在下面的場景中，我們可以看到過牌的EV比下注更高，但Solver傾向在這手牌下注：
為了解釋這類情況，我們首先需要瞭解賽局理論的基本原理。
混合策略的法則
在完美均衡下，混合策略應該始終具有相同的期望值。也就是說，當一手牌混合了兩個或多個行動時，這些行動的期望值應該相等。但為什麼要故意選擇一個更差的策略呢？一個真正完美的策略絕對不會「為了平衡而犧牲期望值」，這是納許均衡的一條硬性定律。
在上面的例子中，我們看到Solver在過牌、下注 27%、73% 和 127% 之間混合了 A7o 策略。然而，這些行動的期望值並不相同。那麼，為什麼我們的解決方案中會出現這種情況呢？為什麼用 A7o 過牌被認為是「不準確的」，而它同時又是期望值最高的行動呢？
Solver中的雜訊
在實踐中，GTO 解答無法達到百分之百的精確度，它們會被計算到一個特定的可剝削性門檻。
整個解答的可剝削性越低，其準確度就越高。我們用一個稱為「納許距離」（Nash Distance）或 dEV 的指標來定義解答的準確度。舉例來說，一家知名的線上解算器網站通常會將解答計算到約底池的 0.2% 到 0.3% 的精確度，這代表著多大的可剝削性呢？
想像一下，在一個按鈕位（BTN）對大盲位（BB）的場景中，底池大小為 5.5 個大盲注（BB）。這意味著最佳策略每手牌最多可以從這個解答中剝削 5.5 的 0.3%，也就是 0.017 個大盲注。這個程度的剝削性，已經遠遠超出了人類玩家的能力範圍。
這就是我們所說的「Solver雜訊」，Solver並不總是會選擇 EV 最高的動作。如果能完美準確地求解，這種噪音就會消失，所有混合行動的 EV 都會相同。
在你選擇一條從未玩過的行動線下，你可能會注意到巨大的 EV 差異，這是為了提高效率，求解器會在求解過程中儘早停止計算被壓制（0%）的行動線，這是正常的，儘管這些行動線中的策略和期望值會降低準確性。
可剝削性
好的，那這是否意味著期望值最高的行動永遠是最佳選擇呢？
不盡然，針對這種精確的策略時，它確實是最佳選擇。然而，如果你總是用A7o過牌，那麼理論上，大盲位的玩家可能會調整他們的策略，使得過牌的期望值反而降低！請記住，Solver 混合各種行動是為了保持不可被剝削性。
如果我們將上述例子計算到完美精確度，過牌仍然會是期望值最高的行動嗎？
對於 A7 牌型，可能會發生兩種情況：
- 過牌的期望值會趨於更低，並因此不再被使用；或者
- 過牌的期望值會趨於與其他下注選項相同，並可能以某種頻率繼續被使用。
在沒有計算到完美精確度的情況下，我們無法確切得知結果。一般來說，低頻率的行動會消失，並導致其期望值降低；而以合理頻率執行的行動則會保留在策略中。這就是為什麼頻率低於 3.5% 的行動會被標記為「不準確」的原因。
停止付給你的對手學費，投資自己永遠是最+EV的選擇！如果您對「學習以德州撲克獲利」或是更進階的內容有興趣，可以點擊諮詢←
範例
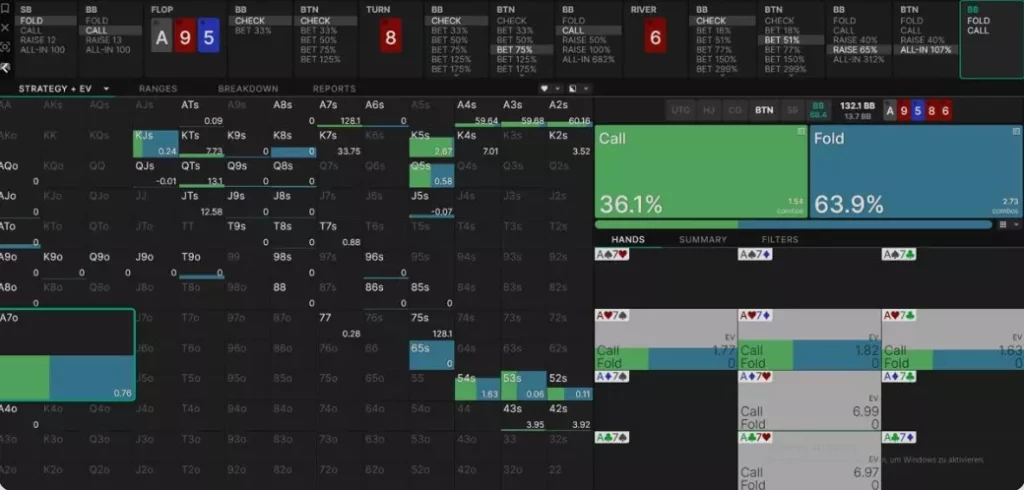
A7o 混合了跟注跟棄牌（即使跟注的期望值更高）
在這裡，我們看到 A7o 在跟注和棄牌之間進行混合策略，然而，跟注的期望值明顯高於棄牌，大約高出 1.7 個大盲注。那麼，為什麼它還要混合棄牌呢？
我們需要將這點放在更大的視角來看待，跟注後，底池大小將達到 200.05 個大盲注，因此，1.8 個大盲注的誤差僅佔底池的約 0.9%。實際上，這個差距比看起來要小得多。當底池變大時，1% 的誤差看起來會顯得大很多。
總是跟注這些邊緣的抓詐唬牌會讓你變得可被剝削，想像一下，如果你用所有這些牌型都選擇跟注，那麼就變成了過度跟注（overcalling），容易被那些價值牌較多的對手所利用。
為何不直接計算出完美精確度的解答？
完美精確度的解答在大規模生產上根本不可行，問題在於，Solver 越接近均衡點，其收斂速度就越慢。從完全未解答到達到 0.5% dEV 所需的時間，大約等於從 0.5% dEV 到 0.25% dEV 所需的時間。
將精確度提高一倍，所需計算時間也會翻倍，而且這還存在報酬遞減的問題。一個精確度為 0.3% dEV 的解答與一個精確度為 0.15% dEV 的解答幾乎相同，並且兩者都仍會存在 Solver 噪音。
另一種方法是建立非常簡單的決策樹（game trees），這會更容易求解，但這也會產生其自身的問題，因為過度簡化你的決策樹會導致人工的失真，這是由於 Solver 利用了該樹的限制而造成的。
所以歸根結底，執著於極高的精確度和微小的期望值並沒有太大意義。無論如何，這些解答的可剝削性都已經遠遠超出了人類的水平，也就是說，就算是精確度不是100%，已經是人類完全無法觸及的程度。
德州撲克GTO實戰應用與學習重點
當你看到 Solver 在不同行動之間進行混合時，你不應該尋找期望值（EV）最高的那個行動，而應該關注頻率最高的行動，這是因為你看到的任何期望值差異都只是Solver 解答中的雜訊。
請將混合行動視為具有相同的期望值，你看到的任何差異都可以被視為誤差範圍（所有牌型的期望值大致都在正負這個誤差範圍內）。
GTO 的重點是找到無法被剝削且期望值最高的策略，你在所有 Solver 解答中都會發現這些微小的誤差，你的目標是描繪出更高層次的策略並發展 GTO 思維，而不是去記憶具體的頻率。GTO 提供的是一個強大的框架，引導我們在面對不確定性時做出最佳決策，並確保我們的策略始終保持不可剝削的本質。
停止付給你的對手學費，投資自己永遠是最+EV的選擇！如果您對「學習以德州撲克獲利」或是更進階的內容有興趣，可以點擊諮詢←
延伸閱讀：
在德州撲克中常被忽視的3個+EV機會點
掌握3大優勢，讓德州撲克變得更簡單
不只是德州撲克，而是更好的自己
參考資料
